Digital Soil Mapping - The fundamentals

Introduction

In recent times we have bared witness to the advancement of the computer and information technology ages. With such advances, there have come vast amounts of data and tools in all fields of endeavor. This has motivated numerous initiatives around the world to build spatial data infrastructures aiming to facilitate the collection, maintenance, dissemination and use of spatial information.

Soil science potentially contributes to the development of such generic spatial data infrastructure through the ongoing creation of regional, continental and worldwide soil databases, and which are now operational for some uses e.g. land resource assessment and risk evaluation (Lagacherie and McBratney 2006).

Unfortunately the existing soil databases are neither exhaustive enough nor precise enough for promoting an extensive and credible use of the soil information within the spatial data infrastructure that is being developed worldwide. The main reason is that their present capacities only allow the storage of data from conventional soil surveys which are scarce and sporadically available (Lagacherie and McBratney 2006).

The main reason for this lack of soil spatial data is simply that conventional soil survey methods are relatively slow and expensive. Furthermore, we have also witnessed a global reduction in soil science funding that started in the 1980s (Hartemink and McBratney 2008), which has meant a significant scaling back in wide scale soil spatial data collection and/or conventional soil surveying.

To face this situation, it is necessary for the current spatial soil information systems to extend their functionality from the storage and use of digitized (existing) soil maps, to the production of soil maps ab initio (Lagacherie and McBratney 2006). This is precisely the aim of Digital Soil Mapping (DSM) which can be defined as:

The creation and population of spatial soil information systems by numerical models inferring the spatial and temporal variations of soil types and soil properties from soil observation and knowledge from related environmental variables

The concepts and methodologies for DSM were formalized in an extensive review by McBratney, Mendonca Santos, and Minasny (2003). In the McBratney, Mendonca Santos, and Minasny (2003) paper, the scorpan approach for predictive modelling (and mapping) of soil was introduced, which in itself is rooted in earlier works by Jenny (1941) and Russian soil scientist Dokuchaev. scorpan is a mnemonic for factors for prediction of soil attributes: soil, climate, organisms, relief, parent materials, age, and spatial position. The scorpan approach is formulated by the equation:

S = f(s, c, o, r, r, p, a, n) + ϵ

or

S = f(Q) + ϵ

Long-handed, the equation states that the soil type or attribute at an unvisited site (S) can be predicted from a numerical function or model (f) given the factors just described plus the locally varying, spatial dependent residuals (ϵ). The f(Q) part of the formulation is the deterministic component or in other words, the empirical quantitative function linking S to the scorpan factors (Lagacherie and McBratney 2006). The scorpan factors or environmental covariates come in the form of spatially populated digitally available data, for instance from digital elevation models and the indices derived from them which include, slope, aspect, MRVBF etc. Landsat data, and other remote sensing images, radiometric data, geological survey maps, legacy soil maps and data, just to name a few. For the residuals (ϵ) part of the formulation, we assume there to be some spatial structure. This is for a number of reasons which include that the attributes used in the deterministic component were inadequate, interactions between attributes were not taken into account, or the form of f() was mis-specified. Overall this general formulation is called the scorpan-kriging method, where the kriging component is the process of defining the spatial trend of the residuals (with variograms) and using kriging to estimate the residuals at the non-visited sites.

Without getting into detail with regards to some of the statistical nuances such as bias issues, which can be prevalent when using legacy soil point data for DSM, the application of scorpan-kriging can only be done in extents where there is available soil point data. The challenge therefore is: what to do in situations where this type of data is not available? In the context of the global soil mapping key soil attributes, this is a problem, but can be overcome with the usage of other sources of legacy soil data such as existing soil maps. It is even more of a problem when this information is not available either. However, in the context of global soil mapping, Minasny and McBratney (2010) proposed a decision tree structure for actioning DSM on the basis of the nature of available legacy soil data. This is summarized in figure below. But bear in mind that this decision tree is not constrained only to DSM at a global scale but at any mapping extent where the user wishes to perform DSM given the availability of soil data for their particular area.

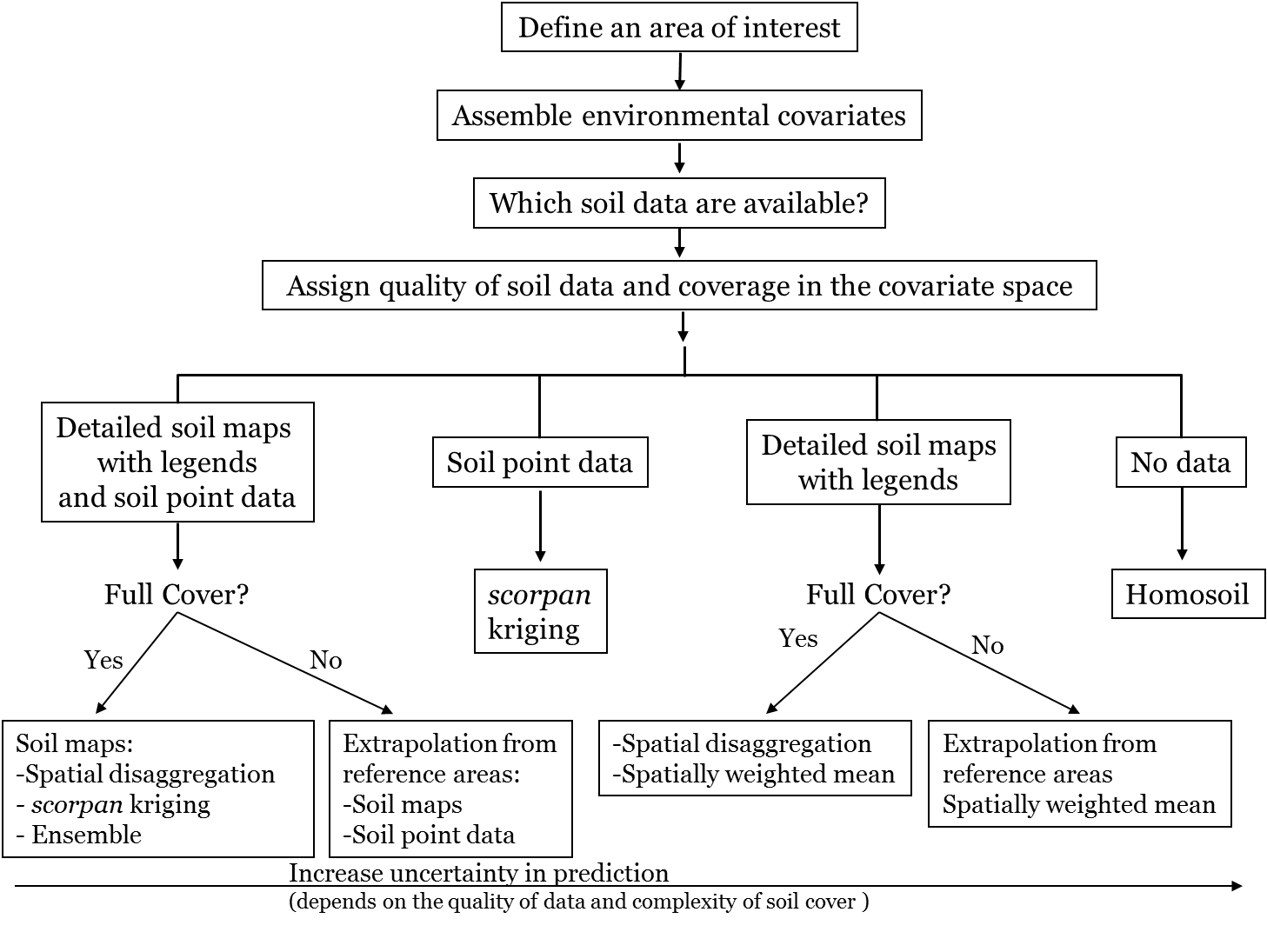
As can be seen from the above figure, once you have defined an area of interest, and assembled a suite of environmental covariates for that area, then determined the availability of the soil data there, you follow the respective pathway. scorpan-kriging is performed exclusively when there is only point data, but can be used also when there is both point and map data available, e.g. Malone et al. (2014).

The work flow is quite different when there is only soil map information available. Bear in mind that the quality of the soil map depends on the scale and subsequently variation of soil cover; such that smaller scaled maps e.g. 1:100 000 would be considered better and more detailed than large scaled maps e.g. 1:500 000. The elemental basis for extracting soil properties from legacy soil maps comes from the central and distributional concepts of soil mapping units. For example, modal soil profile data of soil classes can be used to quickly build soil property maps. Where mapping units consist of more than one component, we can use a spatially weighted means type method i.e. estimation of the soil properties is based on the modal profile of the components and the proportional area of the mapping unit each component covers, e.g. Odgers, Libohova, and Thompson (2012). As a pre-processing step prior to creating soil attribute maps, it may be necessary to harmonize soil mapping units (in the case of adjacent soil maps) and/or perform some type of disaggregation technique in order to retrieve the map unit component information. Some approaches for doing so have been described in Bui and Moran (2003). More recently soil map disaggregation has been a target of DSM interest with a sound contribution from Odgers et al. (2014) for extracting individual soil series or soil class information from convolved soil map units by way of the DSMART algorithm. The DSMART algorithm can best be explained as a data mining with repeated re-sampling algorithm. Furthering the DSMART algorithm, Odgers, McBratney, and Minasny (2015) then introduced the PROPR algorithm which takes probability outputs from DSMART together with modal soil profile data of given soil classes, to estimate soil attribute quantities (with estimates of uncertainty).

What is the process when there is no soil data available at all? This is obviously quite a difficult situation to confront, but a real one at that. The central concept that was discussed by Minasny and McBratney (2010) for addressing these situations is based on the assumed homology of soil forming factors between a reference area and the region of interest for mapping. Malone, Jha, and Minasny (2016) provides a further overview of the topic together with a real world application which compared different extrapolating functions. Overall, the soil homologue concept or Homosoil, relative to other areas of DSM research is still in its development. But considering from a global perspective, the sparseness of soil data and limited research funds for new soil survey, application of the Homosoil approach or other analogues will become increasingly important for the operational advancement of DSM.

What is the intention behind of this DSM course?

These pages cover some of the territory that is described in the figure above, particularly the scorpan-kriging type approach of DSM; as this is probably most commonly undertaken. Also covered is spatial disagregation of polygonal maps. This is framed in the context of updating digital soil maps and downscaling in terms of deriving soil class or attribute information from aggregated soil mapping units. Importantly there is a theme of implementation about these pages; a sort of how-to-guide. So there are some examples of how to create digital soil maps of both continuous and categorical target variable data, given available points and a portfolio of available covariates. The procedural detail is explained and implemented using the R computing language. Subsequently, some effort is required to become literate in this programming language, both for general purpose usage and for DSM and other related soil studies.

The motivation of this course then shifts to operational concerns and based around real case-studies. For example, the book looks at how we might statistically validate a digital soil map. Another operational study is that of digital soil assessment (Carre et al. 2007). Digital soil assessment (DSA) is akin to the translation of digital soil maps into decision making aids. These could be risk-based assessments, or assessing threats to soil (erosion, decline of organic matter etc.), and assessing soil functions. These type of assessments can not be easily derived from a digital soil map alone, but require some form of post-processing inference. This could be done with quantitative modeling and or a deep mechanistic understanding of the assessment that needs to be made. A natural candidate in this realm of DSM is land capability or agricultural enterprise suitability. A case study of this type of DSA is demonstrated in this course. Specific topics of this course include:

• Attainment of R literacy in general and for DSM.
• Algorithmic development for soil science.
• General GIS operations relevant to DSM.
• Soil data preparation, examination and harmonization for DSM.
• Quantitative functions for continuous and categorical (and combinations of both) soil attribute modeling and mapping.
• Quantifying digital soil map uncertainty.
• Assessing the quality of digital soil maps.
• Updating, harmonizing and disaggregating legacy soil mapping.
• Digital soil assessment in terms of land suitability for agricultural enterprises.
• Digital identification of soil homologues.

References

Bui, E.N., and C. J. Moran. 2003. “A Strategy to Fill Gaps in Soil Survey over Large Spatial Extents: An Example from the Murray-Darling Basin of Australia.” Geoderma 111: 21–41.

Carre, F., Alex B. McBratney, Thomas Mayr, and Luca Montanarella. 2007. “Digital Soil Assessments: Beyond Dsm.” Geoderma 142 (1-2): 69–79. https://doi.org/http://dx.doi.org/10.1016/j.geoderma.2007.08.015.

Hartemink, A E, and A B McBratney. 2008. “A Soil Science Renaissance.” Geoderma 148: 123–29.

Jenny, H. 1941. Factors of Soil Formation. New York: McGraw-Hill.

Lagacherie, P, and A B McBratney. 2006. “Digital Soil Mapping: An Introductory Perspective.” In, edited by P Lagacherie, A B McBratney, and M Voltz, 3–22. Amsterdam: Elsevier.

Malone, B P, S K Jha, and A B Minasny B McBratney. 2016. “Comparing Regression-Based Digital Soil Mapping and Multiple-Point Geostatistics for the Spatial Extrapolation of Soil Data.” Geoderma 262: 243–53.

Malone, B P, B Minasny, N P Odgers, and A B McBratney. 2014. “Using Model Averaging to Combine Soil Property Rasters from Legacy Soil Maps and from Point Data.” Geoderma 232-234: 34–44.

McBratney, A B, M L Mendonca Santos, and B Minasny. 2003. “On Digital Soil Mapping.” Geoderma 117: 3–52.

Minasny, B, and A B McBratney. 2010. “Digital Soil Mapping: Bridging Research, Environmental Application, and Operation.” In, edited by J L Boettinger, D W Howell, A C Moore, A E Hartemink, and Kienast-Brown S, 429–25. Dordrecht: Springer.

Odgers, N P, Z Libohova, and J A Thompson. 2012. “Equal-Area Spline Functions Applied to a Legacy Soil Database to Create Weighted-Means Maps of Soil Organic Carbon at a Continental Scale.” Georderma 189-190: 153–63.

Odgers, N P, A B McBratney, and B Minasny. 2015. “Digital Soil Property Mapping and Uncertainty Estimation Using Soil Class Probability Rasters.” Geoderma 237-238: 190–98.

Odgers, N P, W Sun, A B McBratney, B Minasny, and D Clifford. 2014. “Disaggregating and Harmonising Soil Map Units Through Resampled Classification Trees.” Geoderma 214-215: 91–100.